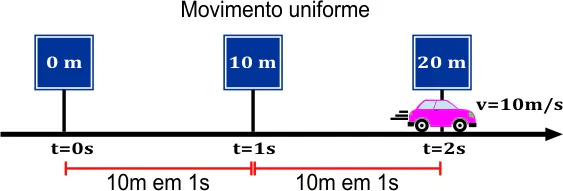
Conceitos iniciais

Para exemplificar esse tipo de movimento, vamos analisar o caso da figura ilustrativa acima: imaginamos que um automóvel se desloca por uma rodovia retilínea, sem curvas ou elevações, a uma velocidade constante. Durante o trajeto, o motorista percebe que a cada 40 segundos ele ultrapassa uma placa de marcação de quilometragem. Isso quer dizer que o motorista percorre uma distância de 1 km a cada 40 s. Se convertemos esse valor, obtemos,

\dfrac{1km}{40s} \dfrac{60s}{1min}\dfrac{60min}{1h} = \dfrac{90km}{h} 

Em outras palavras, pode-se dizer que o automóvel percorreu espaços iguais em tempos iguais, logo, sua velocidade instantânea é igual sua velocidade média. Esse tipo de movimento é chamado de Movimento Retilínio Uniforme ou, como muitos preferem, Movimento Uniforme.

Dissemos que a velocidade instantânea é igual a velocidade média, então, 

v = v_m =\dfrac{\Delta s}{\Delta t}

A função horária do espaço

Na equação anterior, sabemos que \Delta S é uma variação do espaço, assim,

\Delta s = s – s_0

O mesmo vale para \Delta t. Então, se isolarmos a equação da velocidade e manipularmos ela utilzando as definições de \Delta s e \Delta t , ficamos com o seguinte:

\Delta s = v.\Delta t

s – s_0 = v .(t – t_0)

Se considerarmos que, quando iniciamos o estudo dos movimentos, sempre partimos de um t_0 (tempo inicial) igual a zero, e isolarmos o termo que corresponde ao espaço final, temos, 

s = s_o +v.t

Essa equação é chamada de função horária do espaço no movimento uniforme. Agora vamos aplicá-la em um exemplo: na imagem abaixo, podemos calcular a posição do automóvel em instantes de tempo diferentes. Então, supondo que o automóvel saiu da posição inicial de 0 km, qual vai ser sua posição final após 120 s nessa mesma trajetória?